Formula for rotating a vector in 2D

Let’s say we have a point \((x_1, y_1)\). The point also defines the vector \((x_1, y_1)\).

We rotate this vector anticlockwise around the origin by \(\beta\) degrees.

The rotated vector has coordinates \((x_2, y_2)\).

Can we get the coordintes of \((x_2, y_2)\) given \((x_1, y_1)\) and \(\beta\)?

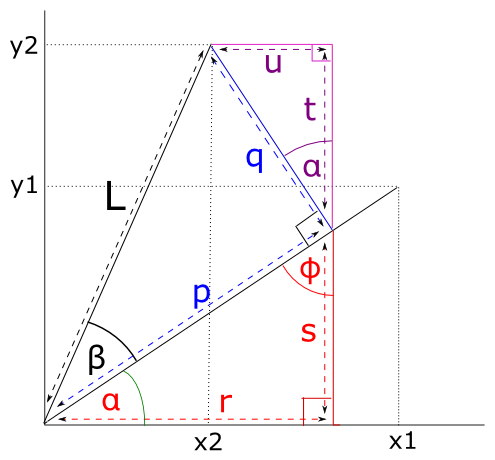
\(L\) is the length of the vectors \((x_1, y_1)\) and \((x_2, y_2)\) : \(L = \|(x_1, y_1)\| = \|(x_2, y_2)\|\).

\(\alpha\) is the angle between the x axis and \((x_1, y_1)\).

We can see from the picture that:

\[ \begin{align}\begin{aligned}x_2 = r - u\\y_2 = t + s\end{aligned}\end{align} \]

We are going to use some basic trigonometry to get the lengths of \(r, u, t, s\).

Because the angles in a triangle sum to 180 degrees, \(\phi\) on the picture is \(90 - \alpha\) and therefore the angle between lines \(q, t\) is also \(\alpha\).

Remembering the definitions of \(\cos\) and \(\sin\):

\[ \begin{align}\begin{aligned}\cos\theta = \frac{A}{H} \implies A = \cos \theta H\\\sin\theta = \frac{O}{H} \implies O = \sin \theta H\end{aligned}\end{align} \]

Thus:

\[ \begin{align}\begin{aligned}x_1 = \cos \alpha L\\y_1 = \sin \alpha L\\p = \cos \beta L\\q = \sin \beta L\\r = \cos \alpha p = \cos \alpha \cos \beta L = \cos \beta x_1\\s = \sin \alpha p = \sin \alpha \cos \beta L = \cos \beta y_1\\t = \cos \alpha q = \cos \alpha \sin \beta L = \sin \beta x_1\\u = \sin \alpha q = \sin \alpha \sin \beta L = \sin \beta y_1\end{aligned}\end{align} \]

So:

\[ \begin{align}\begin{aligned}x_2 = r - u = \cos \beta x_1 - \sin \beta y_1\\y_2 = t + s = \sin \beta x_1 + \cos \beta y_1\end{aligned}\end{align} \]

Luckily this is the same result as wikipedia on rotation matrices.